Table of Contents
Pre-amble
The Malaysian MCO (PKP) was imposed on 18-March-2020 to originally last for two weeks, which was then further extended to 14-April-2020. Whether it will be extended beyond the current deadline is still a question that can’t be answered as of this writing. There are many factors that are unknown (to the public at least) what would be the criterion that the government will use as the benchmark for relaxing or totally uplift the restrictions. If we use the counts of case confirmation as the main indicator, it is still growing at a rate that is hard to predict with good reliability.
Regardless of the finality of the time for the uplifting of MCO, one thing extremely probable is that Covid-19 epidemic is not dying out as fast as everyone wishes. There are many possible reasons for why this to be the case: approach of containment (such as the MCO itself) is not full-proof (i.e. it is always less than 100% effective); aggressive testing of susceptible or infected person takes time and efforts; contact tracing is hard and require massive systems to implement with high effectiveness; the dynamic behavior of the virus is not fully understood and known (at least for now); and finally, human behaviors are not easily predicted.
Assuming that MCO will not last forever, the question is at our personal level or community level, what should be our guide of how to continue our life and works? The purpose of this article is to provide some benchmark which might be useful for us to use as a guide.
Naive empiricism
Before proceeding further to our main discussion, we need to digress a bit here, to highlight a few pertinent issues in regards to efforts to forecast and model Covid epidemic.
Modeling Covid-19 epidemic is extremely precarious, mired with errors (model error and errors in the models), due to many unknown (or inestimable) parameters and weak reliability of assumptions. What we are facing (as humanity) is a Systemic risk of humongous scale, which exhibits an extreme fat-tailed process exemplified by the non-linear behavior of the spreading phenomenon. It is still unknown at the current stage, whether the “fat-tailness” is due to the pathogen’s behavior (which could be understood with more research), or due to the increased connectivity of human beings over the last few decades, or both in combination.
What we have described above fits perfectly into the definition of Dynamic Complex Systems, where the complexity lies in the high number of factors that need to be taken into consideration, the depth of sufficient information required to understand these factors and to understand the relations between these factors (causal, feedbacks, etc.). Under the extreme condition of a highly complex environment, what we have is a systemic failure of many systems. The underlying purpose now is not even about saving the healthcare system, the economic system or other systems, rather it is about saving humanity - on which other systems emanate upon. Saving humanity here does not imply human extinction, instead, it is about “ruin” - where the devastating effects will put the entire humanity in ruin (loss of life, loss of income, loss of confidence, etc).
In the face of such risk, it is dangerous and extreme carelessness for us to take the approach of naive empiricism, that is to rely on forecast and estimates based on “little amount of data” (given many unknowns), “past historical data” (given past epidemics and other data), “forecasting too far to the future” (given too many errors in estimates). There are a few red flags which should caution us at the moment (from heavy reliance on forecasts and estimates): underestimation of spreading rates relates largely to high connectivity among human, which means once we go back to our “normal activities”, the spreading could come again in a big number; the disease reproduction ratio, can’t be estimated with confidence due to existence of “superspreader events” (hence fat-tail distributions); asymmetric uncertainties - effectiveness of policies (such as MCO) is not clear and known, testing is not a perfect activity, and yet inactivity leads to larger ruins.1
Distancing measures post-MCO
Regardless of the risks and dangers of Covid epidemic, human needs to get back to their feet - and thus, the last thing that we need is paranoia. Panic, distress, and chaos - are all part of any crisis - which needs to be averted. All could be reduced if the public and people could be educated about what they should and could do.
For this purpose, we will attempt to perform simulations to understand few dynamics which might help to guide us what could be done by the community post MCO in regards to human mixing and distancing. We pick on this subject purposely due to few reasons:
From many perspectives of medical, complex systems, contact tracing, and testing, restricted movements, etc., the key parameter is about the reduction of human connectivity.
From network science (graph theory), given that the best guess of the spreading formation (network) follows power laws distribution - we can safely assume that there exists a certain threshold of this connectivity - for spreading to be under control.
Very likely, from any form of measures, human distancing proves to be the most effective and efficient method of eventual disease spreading reduction (and hopefully total elimination). Furthermore, with the combination of other methods (tracing and testing - disease detection, quarantine, and isolation - disease spreading prevention, immunization - if it becomes available and affordable, and a plethora of other methods), human distancing is something that can be done without any “external interventions”, and hence if it works, it works well with least cost possible.
With the above points in mind, let us then delve into detailing the subject.
Define human distancing
Human distancing is NOT social distancing as defined within the current context of epidemics. Social distancing (under epidemics) is defined as “staying away from mass gatherings or crowded places, and keep a distance of six feet or two meters away from other people”.2 Under this definition, practically there are no works can be done, except through online communications - which in the case of Malaysia, we are not fully prepared to embrace it en masse.
First and foremost, our definition of human distancing is as follows: “keep the number of people that you deal with daily (exclude your family) to be NOT more than X persons, for a period of Y time”. X and Y in combinations are the measures of the distance.3 In a plain statement, this could be as follows: “within a period of two weeks, I only (strictly) deal (i.e. meet, sit next to each other, converse, etc.) with a maximum of twenty people whom I know who they are (example colleague in an office) in the normal course of work”.
How do we come out with such a definition? We derive this from “human network” theory of disease spreading phenomena, which identify that spreading events mainly (more than 95%) took place through contacts which took place via heterogeneous mixing of people of a certain size (number of people gathered) and over a certain period of time.4
Based on this notion, we can safely say that (at least based on currently observed phenomena), that in the case of Malaysia, the human distancing is: “to keep the number of people that you deal with daily (exclude your family) to be NOT more than TWENTY PERSONS, for a period of TWO WEEKS”.5
How do we come out with such parameters?6 The answer lies in simulations of the human network under the Malaysian Covid scenario. As we have presented before, we have shown that the Covid spread can be shown as a network of human contacts (Tabligh cohort), under which the network follows a power-law distribution of degree approximately equals to 2.
The spread is shown in Figure 1 (as shown in the previous article).

The question that we want to know is: what is the upper limit on the number of links (edges) to be eliminated from the graph to convert it to behave more like a random graph instead of a scale-free graph? The answer (rounding to nearest easy number) is twenty. If we remove the nodes with more than 20 links, suddenly the graph is no longer having the shape of Figure 1, but instead, it becomes almost a random graph, as shown in Figure 2.7
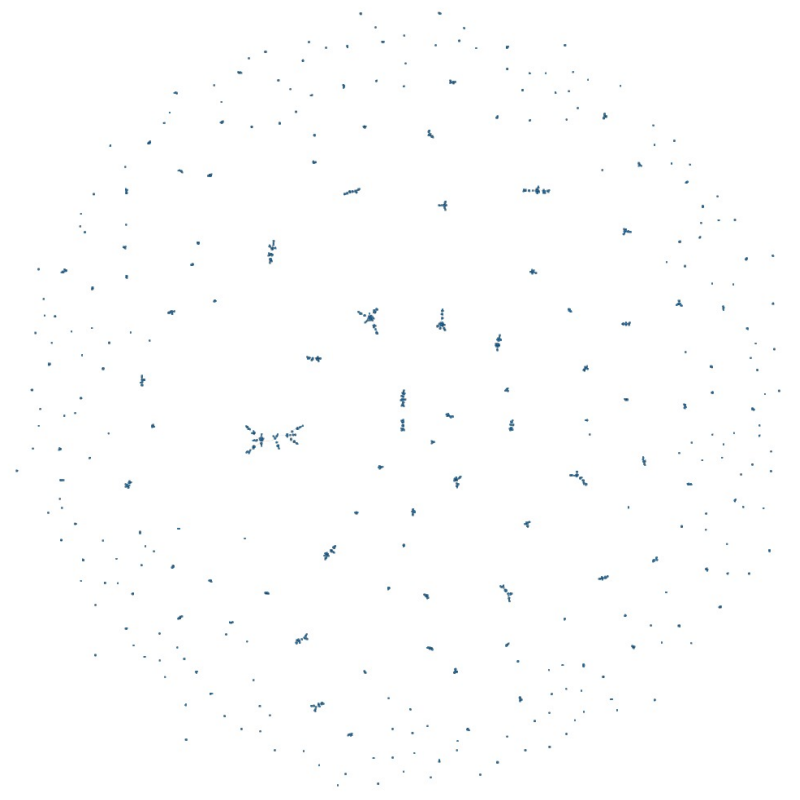
The difference between Figure 1 and 2 is obvious: The nodes are no longer connected as a “big single hub” - which means, as far as Covid is concerned, there are no more large widespread of the disease, and there are clear distances between the people (in the cohort). What this implies is that if the actors strictly practice limiting the number of people they interact with on regular basis over a certain defined period, the probability of spreading (the pathogens) are eliminated to almost zero rather dramatically. However, the danger here is the tipping point - what is the largest number of mixing under which condition the large hubs to start to appear again? The answer is 150 or above.8 How do we come up with 14 days? It is the maximum end of the incubation period of Covid.9
Conclude
What we try to demonstrate here is a simple use of network theory (of human behaviors network) could be helpful to derive some heuristic rules which could be implemented as a measure of human distancing among the people in the face of the Covid epidemics. The rules derived are robust to perturbations, provide a strong basis of controls in a dynamic setting, and reduce the risks of cascading systemic failures. At least, that’s what we could learn from the network theory point of view. More practical and realistic applications are of course up to our human ingenuity as a society, and the final determination is always up to the Maker.
For detail exposition, please refer to Norman, et. al.,Systemic Risk of Pandemic via Novel Pathogens - Coronavirus: A Note, New England Complex System Institute, January 26, 2020. http:://necsi.edu/systemic-risk-of-pandemic-via-novel-pathogens-coronavirus-a-note↩
Definition by US CDC. https://www.cdc.gov/coronavirus/2019-ncov/php/risk-assessment.html↩
Strictly, it means that \(d = f(X|Y)\)↩
This is called the Percolation Theory of networks, where the spreading will fail quite drastically (non-presence of giant components) if the networks meet certain threshold values↩
Note that other measures such as no physical contacts, wearing face masks, sanitization would be helpful and advisable to be practiced↩
We will provide a verbal proof here. For details, please refer to Barabasi, Albert-Laszlo, Network Science, Cambridge University Press, 2016↩
In physics, what we are interested here is to find the region of phase transition, where below the phase transition the system exhibits a different character as opposed to above the phase↩
Exact number is 164, but we round down to 150. The reason why we chose 20 is simply the most logical smallest number, where any number below that does not have any significant difference (i.e. further improvements), and large enough to be meaningful. Why we didn’t choose 150 (the upper bound) instead? It is just too close to the Percolation point. Why not choose a number larger than 20, say 50? Under 50, the probability of having a hub with 50 is possible, whereas the largest hub under 20 is 20, which is smaller and easier to manage, compared to 50. For argument sake, any number above 20 and below 164 is within the safe range. But in practical terms, it is harder to manage a set of people above 20, and for that reason 20 is chosen as a practical number. Furthermore, it has been found in other studies that 20 is the average number of people per day that an average working person meets on a day.↩
We could use 21 days (three weeks), but then it seems too long (hence to strict), or 7 days (which is the mean incubation period, which is too short)↩